
高校受験対策 数学 関数1 交点 面積 王道パターン Mp3
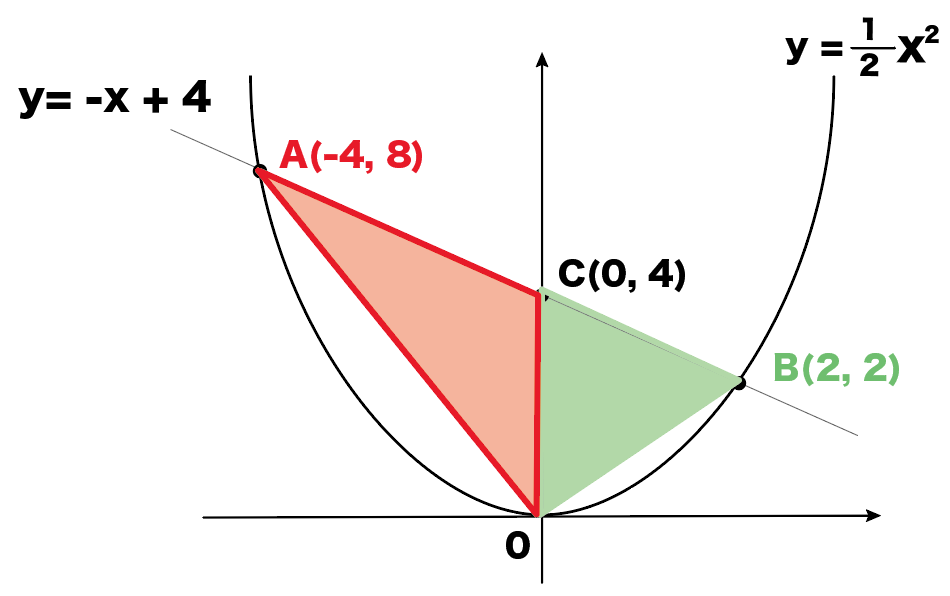
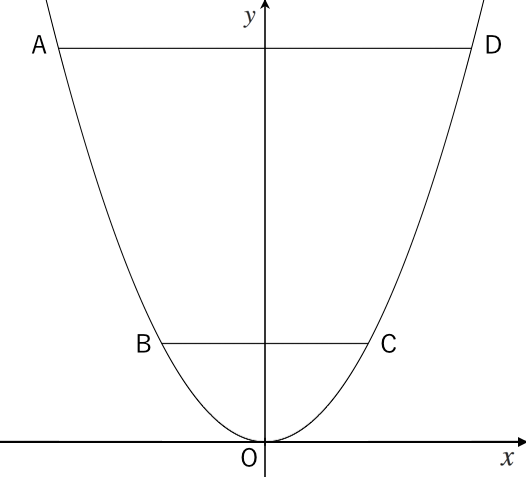
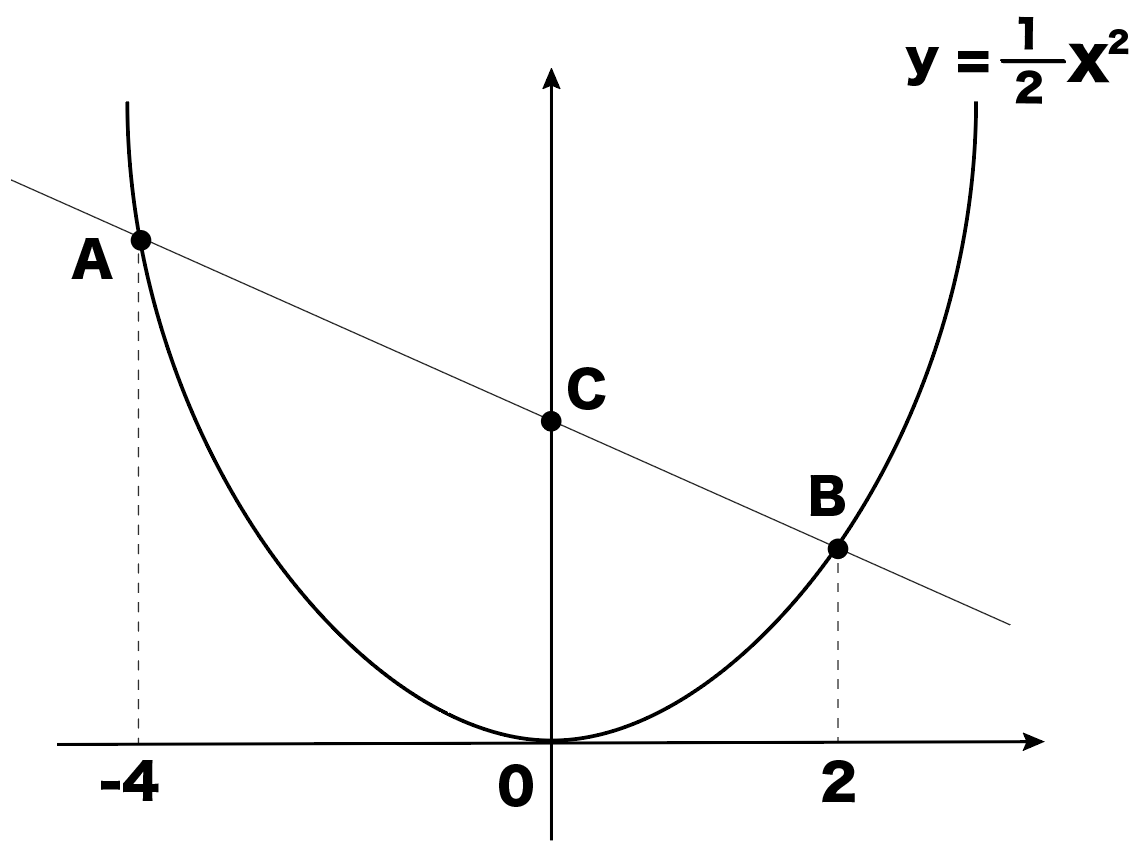
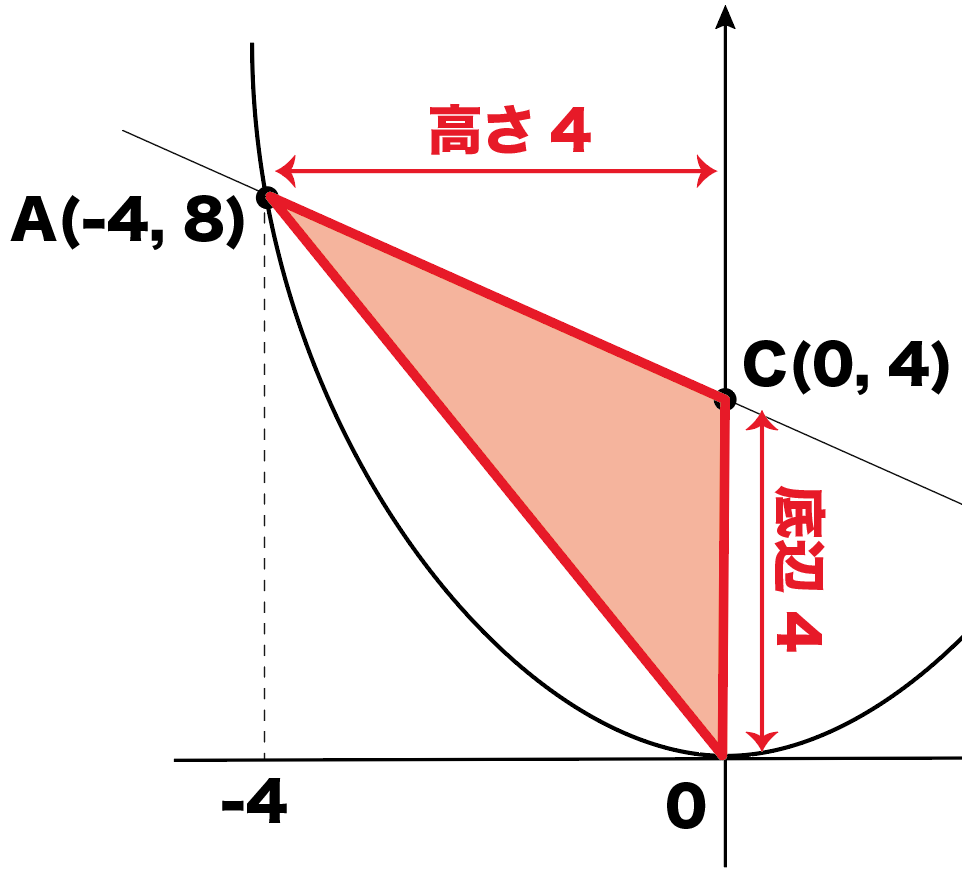
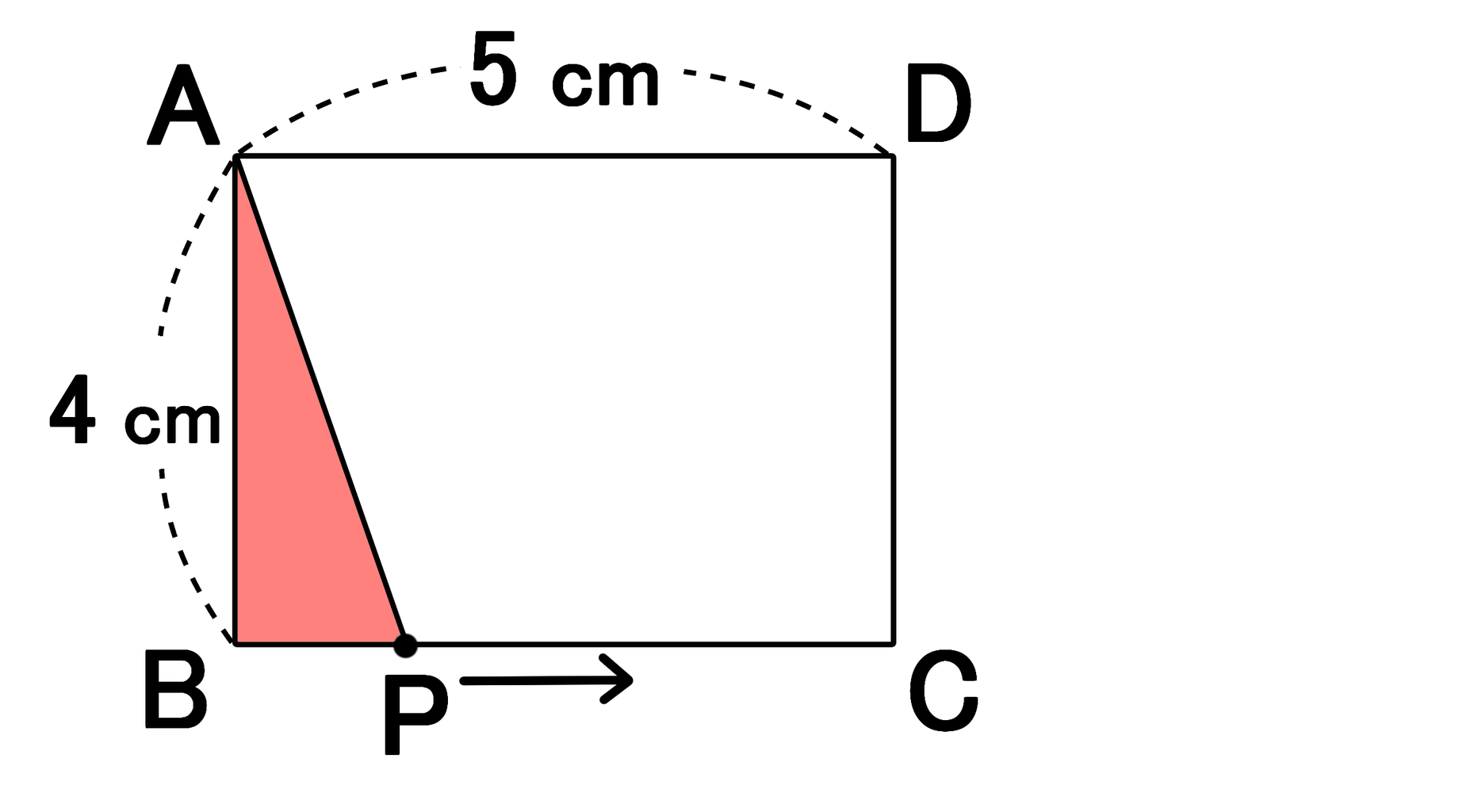
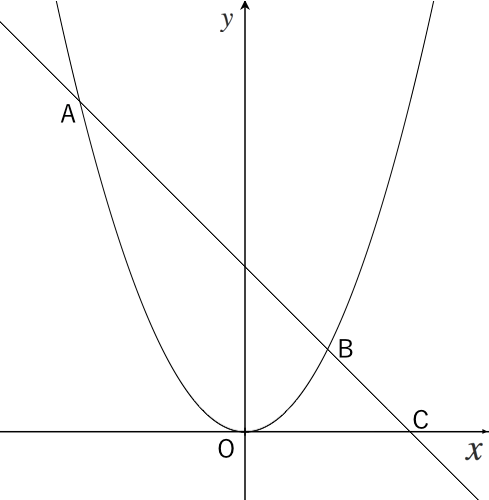
例題②図のように、関数 $\textcolor{green}{y=\frac{1}{2}x^2①}$ と関数 $\textcolor{green}{y=x4②}$ のグラフがある。 $\textcolor{green}{2}$ つのグラフが点A,Bで交わるとき、次の問いに答えなさい。 (1) 点A,Bの座標を求めなさい。 交点の求め方は $1$ 次関数の場合と同じ連立方程式の代入法で解きます。 二次関数のグラフ上の面積を二等分する応用問題(応用1) 目次 問題 解説 a の値を求めなさい。 BCDの面積と四角形ADCPの面積が等しくなるDの座標は?
数学 関数 グラフ 面積
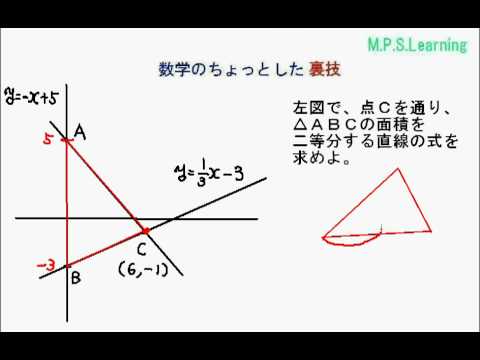
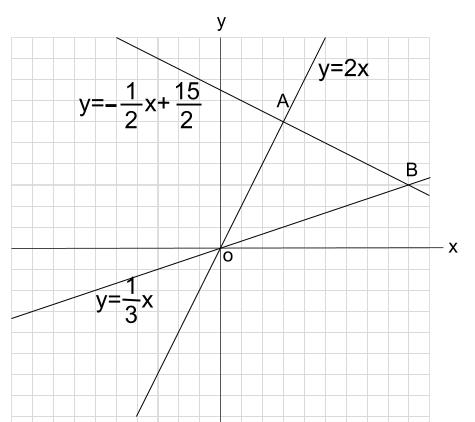
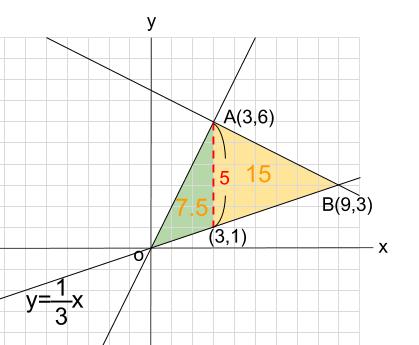
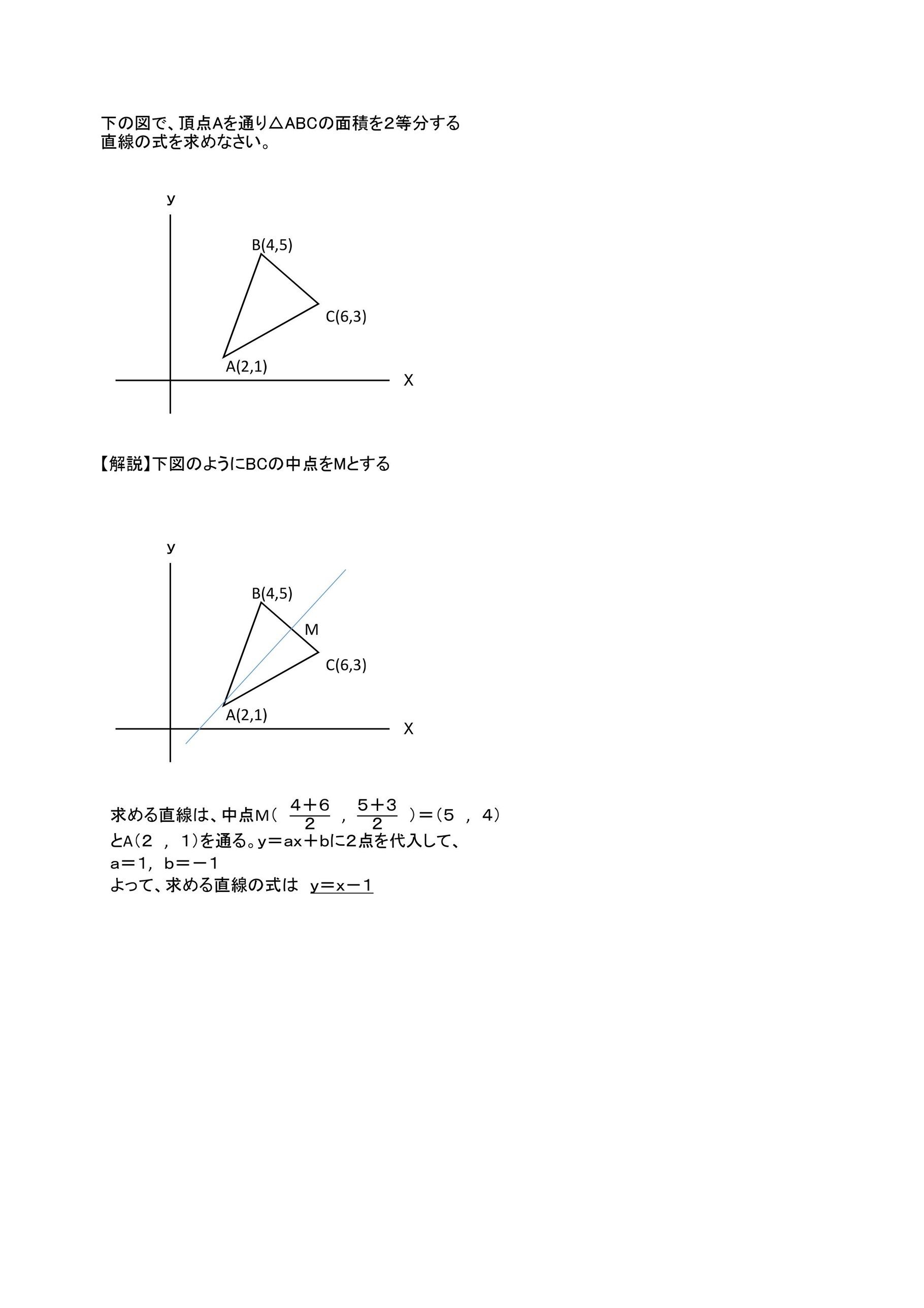
数学 関数 グラフ 面積-今回は一次関数の単元から グラフ上にある三角形の面積を求める という問題の解き方について解説していきます。 また、応用編ということで、三角形を2等分する直線の式は?という問題についても一緒に考えていきましょう! 面積を求めるとなると媒介変数表示された曲線のグラフの面積の求め方 STEP1: 媒介変数表示された曲線のグラフを書く .正負がわかれば増減表が不要な場合もあります. STEP2:該当範囲を積分する.ほとんどの場合,媒介変数で置換積分します.グラフの折り返しの有無に注意
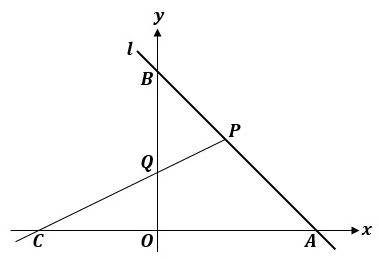
1次関数とグラフの問題 東久留米 学習塾 塾長ブログ
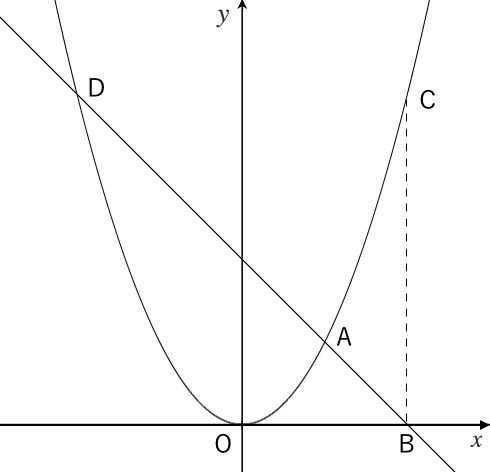
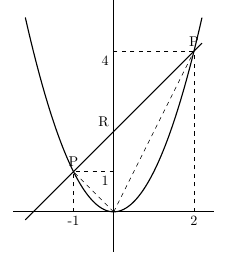
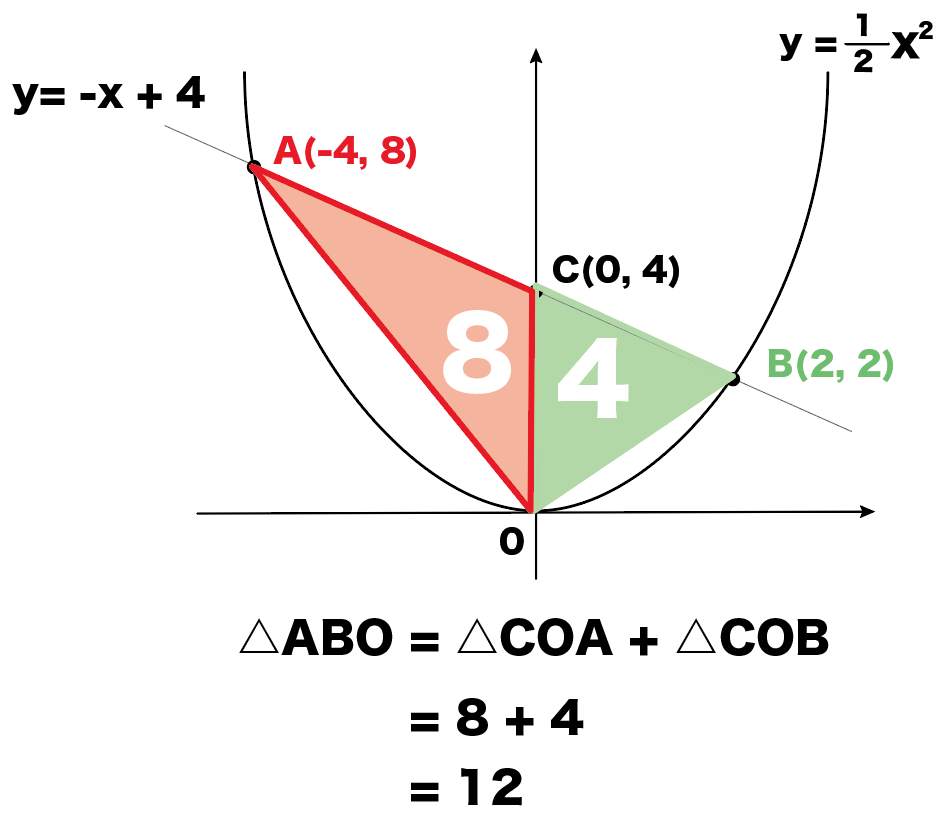
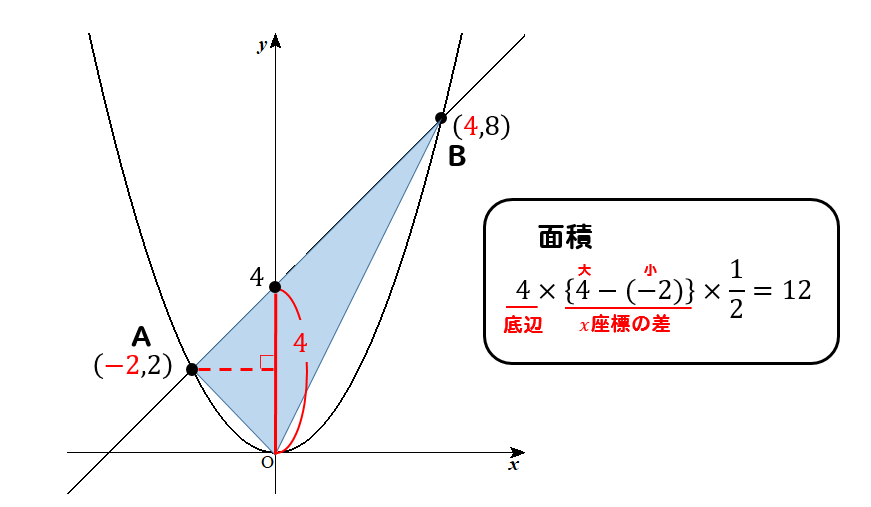
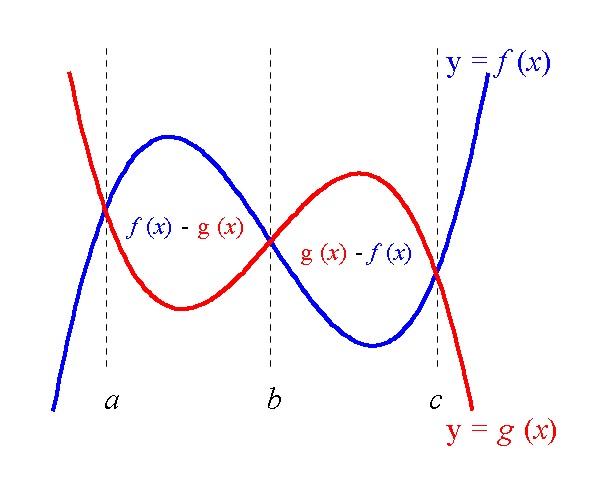
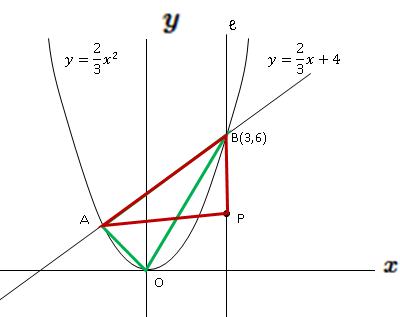
2次関数 y=x 2 のグラフと直線 y=2x+3 の交点A,B及び原点Oでできる OABの面積を求めなさい. OABの面積= ・・・(答) y=2x3だから切片は3 → OP=3 放物線と直線の交点A,Bの座標は連立方程式y=x 2 (1), y=2x3(2)を解いて求める。 こうすれば結果的に2つの関数の間の面積(2つの関数が囲む面積)を求めることになりますね。 1 度具体的にやってみましょう。 2 つの関数として \(f(x)=x^25x1\) \(g(x)=x^23x5\) を考えます。これは図を書くと になりますが、この間の面積を求めてみます。 3次関数のグラフと面積~大切なのはx軸より上か下か~ 今日はこんな問題を取り上げようと思います。 つい、最近授業で扱いました。 曲線 と 軸で囲まれた部分の面積を求めよ。 ここでまず確認しておきたいのが, 曲線と軸に囲まれた部分の面積 につい
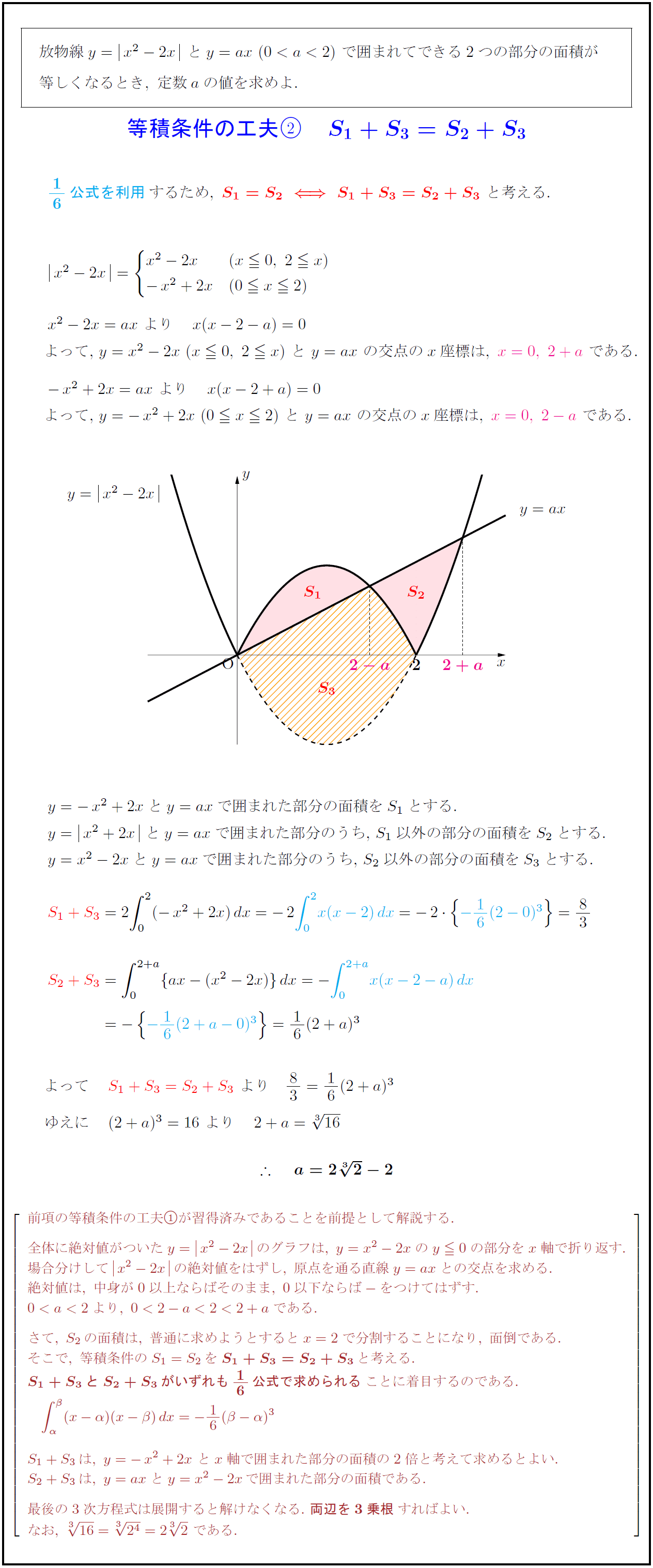
ここまで, \(f(x) \geqq 0\) の場合と \(f(x) \leqq 0\) の場合に分けて,関数のグラフと \(x\) 軸,さらに \(y\) 軸に平行な直線で囲まれた図形の面積を求めてきました。 それをそのまま使ってもこの図形の面積を求めることはできるのですが,少々面倒な計算になりそうです。中学数学のグラフと図形練習問題です。授業の予習、復習から定期テスト対策、受験勉強に活用してください。 (0,12)である。三角形aopの面積が36になるときの点pの座標を求めよ。 関数 例題 グラ 接線とグラフ・軸が囲む面積と体積 <この記事の内容>:前回「接線の方程式の求め方と接点が未知の場合の対処法」の記事で、接線の求め方などを詳しく紹介しました。 今回はその続編として、 ・その『接線と関数のグラフ、軸などに 囲まれた部分の面積 』をうまく求める方法を解説し、
数学 関数 グラフ 面積のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  | |
 |  | |
「数学 関数 グラフ 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「数学 関数 グラフ 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「数学 関数 グラフ 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「数学 関数 グラフ 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「数学 関数 グラフ 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「数学 関数 グラフ 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「数学 関数 グラフ 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「数学 関数 グラフ 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「数学 関数 グラフ 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「数学 関数 グラフ 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「数学 関数 グラフ 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |





0 件のコメント:
コメントを投稿